Projects | UGV Design Heuristic Optimization

Heuristic Optimization of an Energy Autonomous UGV

Sungrove in Mobile State

Sungrove in Harvesting State

Sungrove in Mobile State

1/5

Nature-Inspired Optimization

Spring 2018

Here I apply particle swarm optimization (PSO) and a genetic algorithm (GA) on a previously proposed design for a solar powered unmanned ground vehicle (UGV) - The SUNGROVE. The proposed design was originally optimized to find the optimal design parameters to maximize certain performance parameters of the UGV. In the report provided below, this optimization is replicated with the same objective function, constraints, and variable bounds as the the original optimization, however, the optimization method is replaced with GA and PSO algorithms in an attempt to arrive at another solution.

Genetic Algorithm

The genetic algorithm (GA) is a nature-inspired algorithm that mimics the concept of survival of the fittest for evolution.In nature, genes heavily influence whether or not a specific individual survives against predators and the environment. Most of the genes are identical amongst individuals in a species, but slight variations in the genes affects the color, awareness, reflexes, etc. of a certain individual in that species.

These principles are used as the basis for the genetic algorithm. A randomly selected set of candidate designs is chosen as the sample population. A fitness value is assigned to each candidate by evaluating the value of the objective function using the candidate’s design variables. After many iterations, the algorithm converges upon an optimal design set.

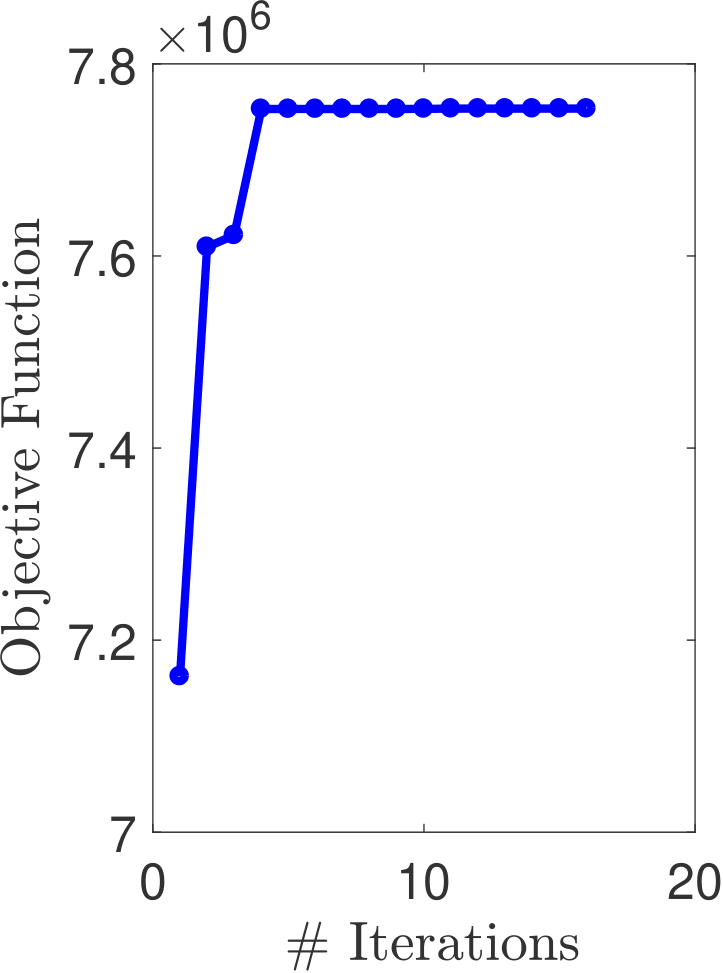
Particle Swarm Optimization

The general particle swarm optimization also works with an iteratively changing set of candidate designs in a population set. The design candidates can be considered as particles in n-dimensional space. A random set of particles are generated, and the objective function evaluated with their design parameters. With each iteration in the algorithm, each particles position in space is updated with its new velocity, based on the current best global (best across all candidates) and local (the candidate's personal best) values of the objective function, along with their individual inertias. After a specified number of iterations, the set of n design parameters with the best objective function value is chosen as the solution.

Project Requirements